代码 学习

CSP-S 2019 Emiya家今天的饭 题解

本文的作者是 Azrl.
发表于 即将逝去的 洛谷博客.和 heiyedao 博客(是这个名字吗).

前言

这篇题解写于 2022 年 11 月 19 日 .鉴于我当时精神状态不是很好,加上我本身又很蒻, 大家就凑合着看吧,当个乐子,估计您们都会觉得我很屑的.
今天是 2022 年 12 月 1 日.将笔记本里的题解以博文的形式放在互联网上.防止笔记本被偷掉造成的永久性失忆(当然,没人屑于偷我的笔记本).
顺便也当作我练习markdown的一次机会吧.

Update 2022年12月2日,增加图片解说.优化了文章的latex和布局.

Update 又是2022年12月2日,晚上十点半.我忽然想起来我图片好像画假了然后趁老师不注意下晚自习又冒着生命危险溜回来改好了,大家快夸我敬业(

正文

Problen5664Discribe

题目链接:Luogu P5664

Solution

老早看这道题不顺眼了,今天干了他.

a1

我们发现直接去枚举每一列中已经选择了的元素会导致复杂度变得很大.因为我们的答案中可能有很多m列,每一列都选择了1个元素这样的情况.而题目只要求了任意一列不允许出现选择的元素数量大于已选择元素一半的情况.并且仔细思考会发现,这样违规的列,最多只会有一个,因为每一行最多只能选择一个元素. 所以我们可以转而对不合法的情况数目进行统计,分别枚举某一个不合法的列.考虑DP.

我们设 dp(i,j,k) 为 当前在的列数为col,已经考虑了i行,当前列有j个元素被选定,其他列总共有k个元素时,不合法的方案总数. 然后转念一想,我们只需要考虑j > k 时的状态即可,因为当 j <= k时,该状态的贡献都为零. 则我们重设 dp(i,j) 为 当前在的列数为col,已经考虑了i行,当前列比其他列多了j个元素时,不合法的方案总数.

接下来是推转移方程.

当前状态的来源有三个:

  • 在选择完i-1行之后,col列已经比其他列多了j-1个元素.这次仍然需要选择在第i行col列的元素.
  • 在选择完i-1行之后,col列已经比其他列多了j+1个元素.那么根据定义.这次需要选择不在第i行col列的元素.
  • 在选择完i-1行之后,col列已经比其他列多了j个元素.那么本次不需要选择元素.(第一行除外,需要特判).

第一种情况.此时我们需要选择第col列的一个元素,以满足需要.

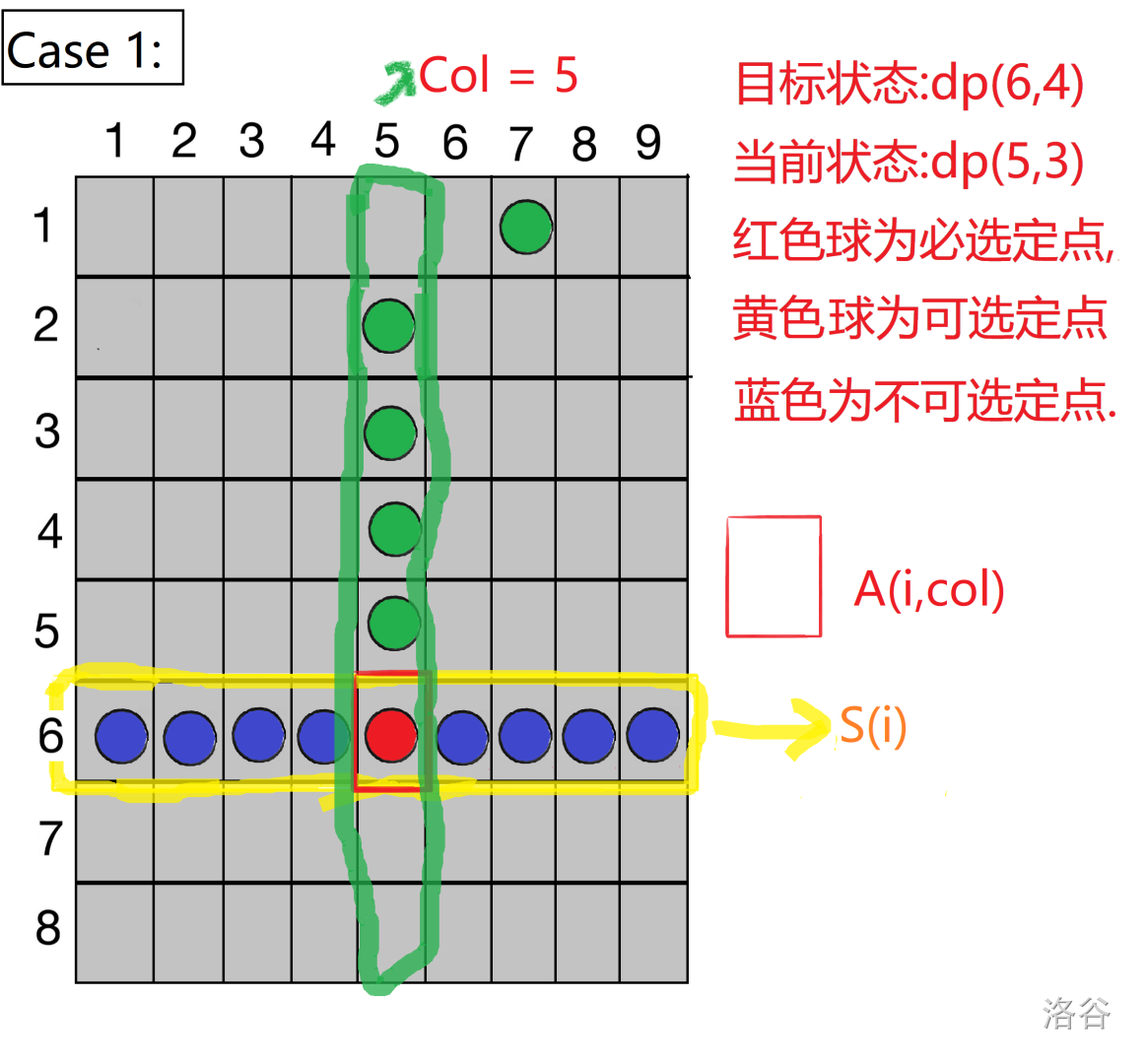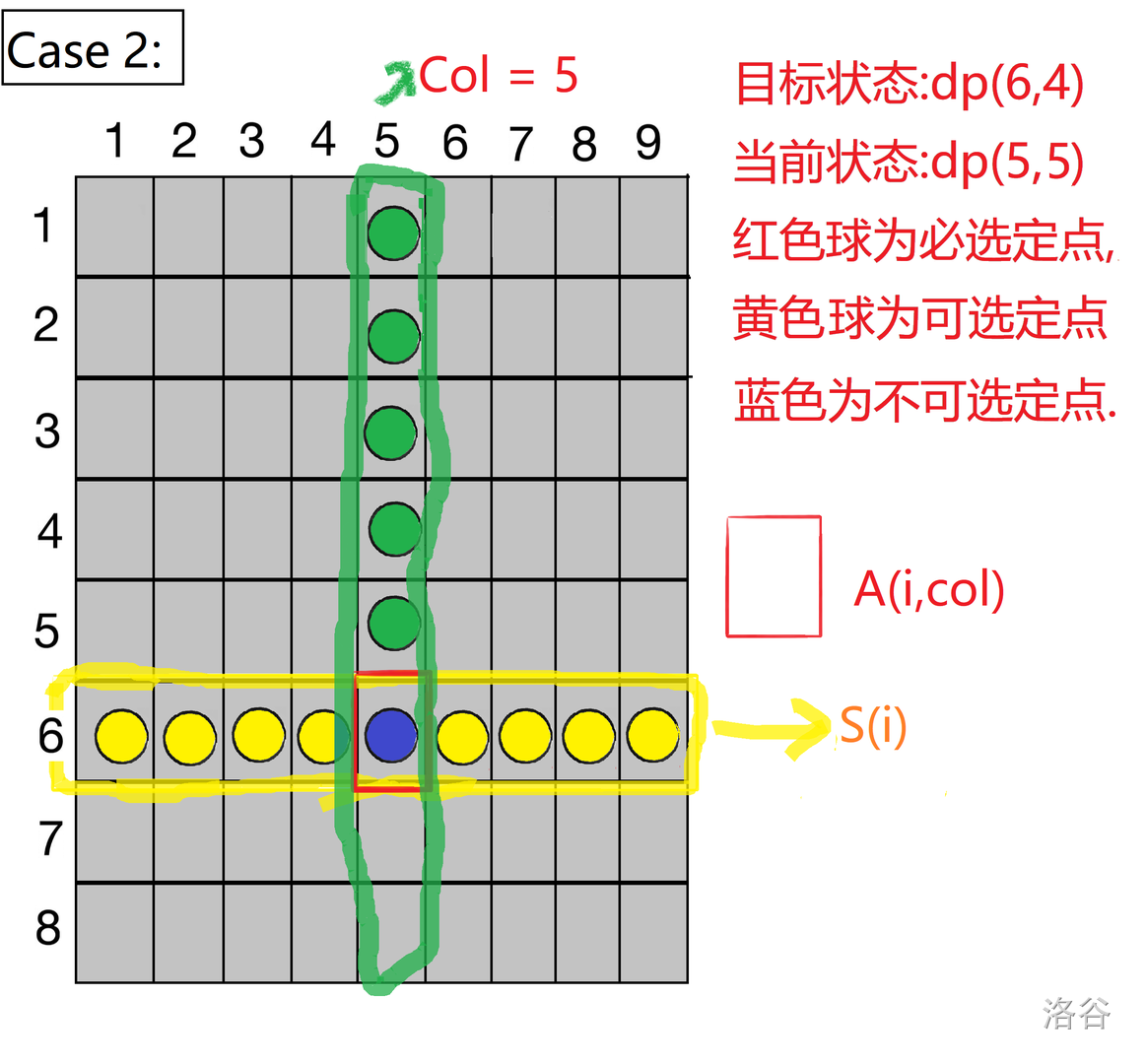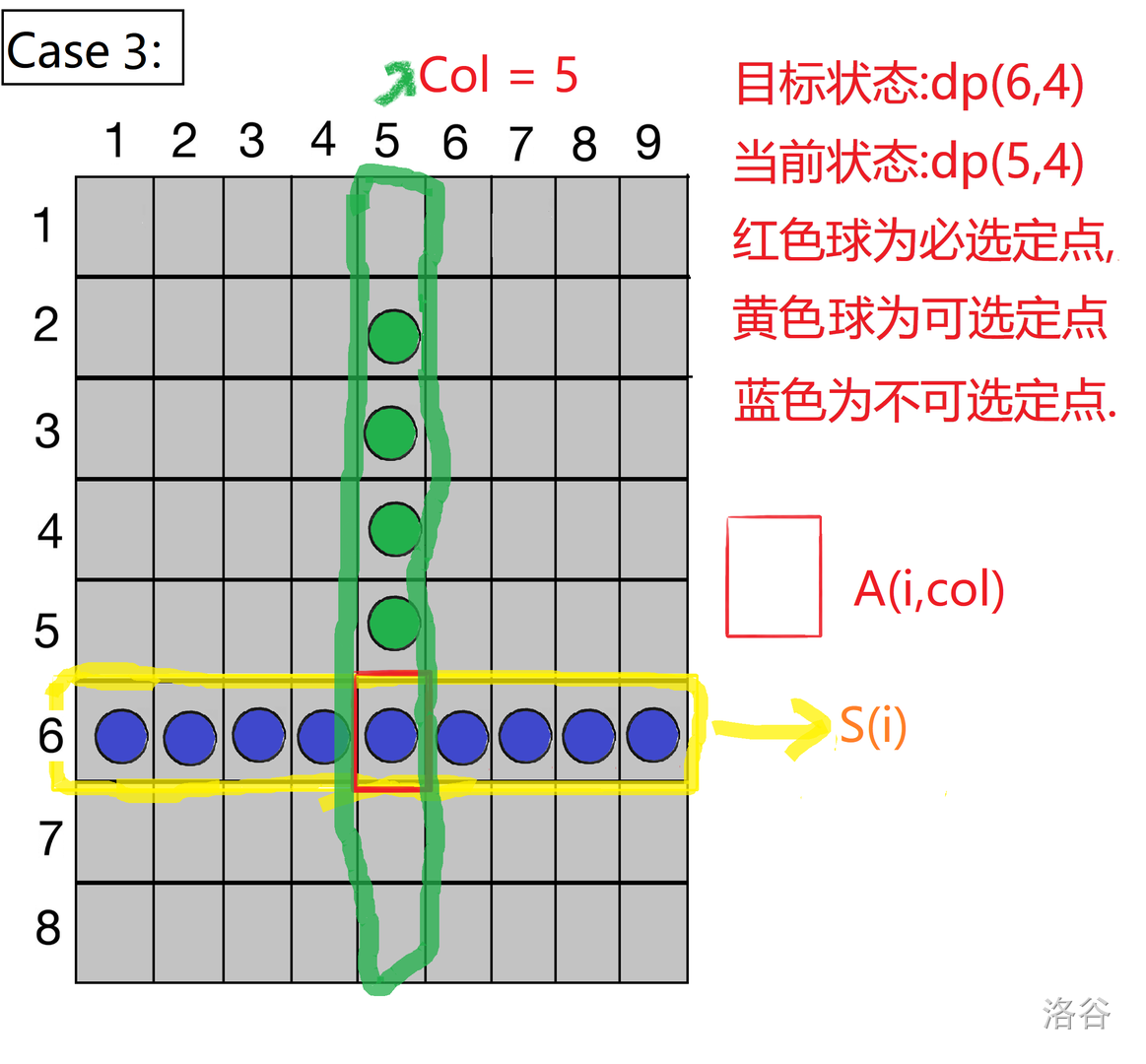
case 1 第二种情况.此时我们应选择除第col列之外的任意一个元素,以满足需要. case 2 第三种情况.此时我们不应该选择任何元素,以满足需要. case 3

综上,则转移方程为:
a2

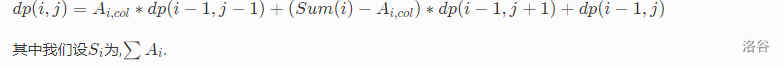
之后我们要求出没有限制情况下的总方案数.
设G(i,j) 为:总共选定了前 i 行 j 个数的方案数.
则递推式为: G(i,j)=G(i-1,j)+G(i-1,j-1)* S(i) .

统计答案.则总方案数等于合法总数减去不合法总数.
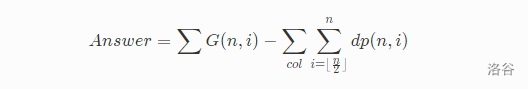
answer

我的代码.码风极其差,人傻常数大

记得取摸,统计答案要用long long. 


/*
Date:2022-11-20 11:56:50 
100pts,Accepted
Writen by Azrl.
*/

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn = (int)(1145.14*3);
long long a[maxn][maxn];
long long dp[maxn][maxn];
long long g[maxn][maxn+1];
long long s[maxn];
const int mod = 998244353;
int n,m;

int main(){
    //ios::sync_with_stdio(false);
    //cin>>n>>m;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++)
            /*cin>>a[i][j]*/scanf("%lld",a[i]+j),s[i]=(s[i]+a[i][j])%mod;
    }
    long long ans = 0;
    for(int col=1;col<=m;col++){
        memset(dp,0,sizeof(long long)*(n+n)*(m+m));
        dp[0][n]=1;
        for(int i=1;i<=n;i++){
           for(int j=n-i;j<=n+i;j++){
               //88pts's Mod question.
               dp[i][j]=(1ll*dp[i-1][j]+1ll*dp[i-1][j-1]*a[i][col]%mod+1ll*dp[i-1][j+1]*((s[i]-a[i][col])%mod)%mod)%mod;
            }
        }
        for(int i=1;i<=n;i++)ans=(ans+dp[n][n+i])%mod;
    }
    g[0][0]=1;// ./..
    for(int i=1;i<=n;i++)
    for(int j=0;j<=n;j++){
		g[i][j] = (g[i-1][j]+(j>0?(g[i-1][j-1]*(s[i]-0)%mod):0))%mod;
    }
    ans=-ans;
    for(int i = 1; i<=n; i++)
	    ans = (ans+g[n][i]+mod)%mod;  
    //cout << ans << endl;//////
    printf("%lld",ans);
    return 0;
}

后记

我一开始的想法是把col缝合进状态中.但是这样没有必要,因为可以重新利用数组.当时的我思想有些混乱,设计出来的状态是将行列一起枚举转移,这无疑会多占用很多空间,并且我还把状态设计错了.并且我一开始数次没认真看题目就写代码,写代码的过程中粗心的错误也连连犯下,这都是要改正的缺点.如果你看到了这篇文章,也请在此时,一起和我反思一下平常点滴的小错误吧.努力克服它,相信生活会变得更好.
顺便说一下洛谷的图床,图片被用户移除之后不会立刻从服务器中删除(这是好事吗

还有606066.xyz这个博客,大家一定要多多支持呀.它的master人挺好的,嗯

说明:这里是heiyedao特供版,为了提供正常的阅读情形,我把一些渲染不出来的latex公式以图片的方式展现,最大的保留了题解原本的样子.当然,可能缩放是有点问题,日后等heiyedao修好再说吧 (催更行为不道义). 并且这个蒟蒻太弱了,不敢公开自己的洛谷博文.

backtop