P1082 [NOIP2012 提高组] 同余方程&P2613 【模板】有理数取余 题解.

本文的作者是 Azrl.
发表于 即将逝去的 洛谷博客.和 heidayo 博客.

前言

这两道题并不难,只是模板题难度.此题解记录的是作者自己对问题的思考进程,或许有一定的参考价值.这篇也算是我,改变过往对数论的看法,向数论挑战的一个开始吧.当然您们还是稳稳地吊打我,只不过这个蒟蒻稍微不那么水货一点,吊打起来会更舒服罢.

啊,既然heiyedao说要给博客加装latex,那我就直接显示公式了.
update: 我来到heidayo才发现heiyedao的确回复了我,并且发了一个latex的分数.我本来想改一下文章,结果点开预览()还是有其他问题.那我还是,用图片版来代替之吧.

测试:Latex效果

$$ Answer = \sum{G(n,i)}-\sum_{col}\sum_{i = \lfloor \frac{n}{2} \rfloor}^{n}{dp(n,i)} $$

阅读本文……呃,或许需要gcd的前置知识?怕是您们又会对此唏嘘不已.

还有,下文里面出现的所有数默认为整数.

那么开始罢.

[NOIP2012 提高组] 同余方程

Solution

一步一步来.
做数论题之前都需要来一口深呼吸.看题目.
!(solution1082_1)[https://cdn.luogu.com.cn/upload/image_hosting/m1fa2kpy.png]
啊,那这可怎么处理?
人们叱诧风云,我为旁观者,见过世人写扩展欧几里得算法(exgcd).然后朝着这方面想,同余式子,到底蕴含着什么道理.

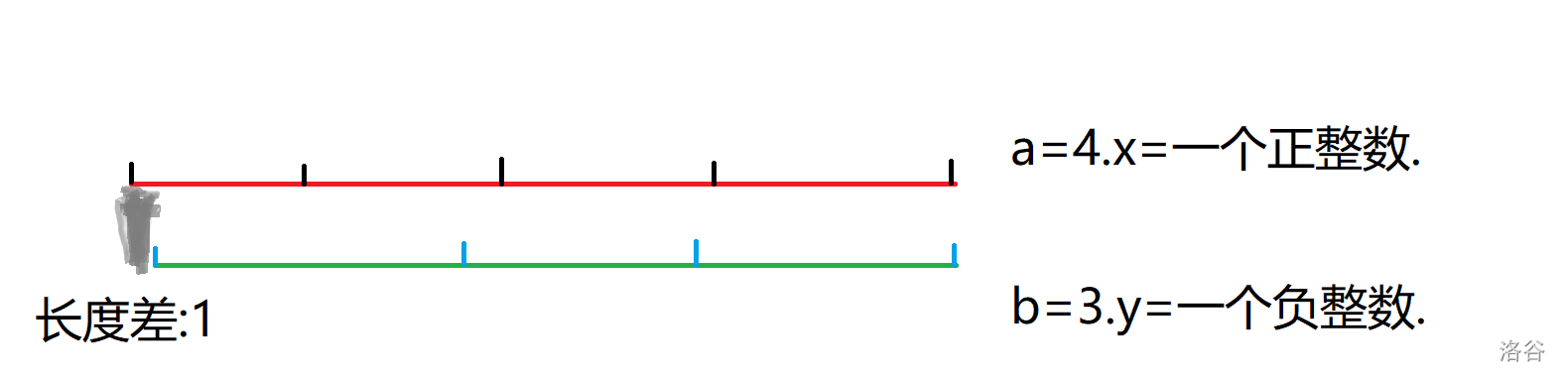
啊.所以那个式子可以顺势写成:
ax + by=1
这长的就像扩欧.不过扩欧求的是ax + by = gcd(a,b) .回到上式,这里的 a,b 必须互质才可以满足条件.那样的话,他们的最大公约数gcd(a,b)才会是1. 为啥呢? 因为有如下定理:
方程ax + by = m 的必要条件为 m \bmod gcd(a,b) = 0.
那这又是为啥呢. 可以稍微证明一下:
由最大公约数的定义,gcd(a,b)可以整除a,b.废话 又因为x,y都是整数,那ax+by就一定是由有限多个gcd(a,b)拼成的,也就是说ax+by一定是gcd(a,b)的倍数.又因为m自己就是ax+by,自然m整除gcd(a,b). 证完.

那自然, a,b 必须互质才可以.
我们可以求出来ax+by = 1的一个可行解,然后试着让x变为可行解集合中的最小的正整数.这一步我们可以通过这样做到:

(x % b + b) % b

为啥呢.我们手玩一下可知, x 递增 b 之后,或者, y 递增 a 之后,都不会出现无解的状况.因为我们有

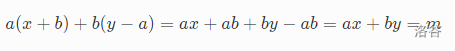
所以操作可行.
至于为啥 x 模 b 之后还要再加上b然后再模一次,这是因为我们要求最小正解.如果 x 是负的,那模b之后其绝对值一定小于 b ,再加上 b 就会变成正的,并且一定是最小的正解.如果x本来就是正的,那就算再加上b,也会被之后的取模运算消掉.所以这么折腾下来的确能得到正确答案.至于y,本题用不到,只是个副产品.

嗯,然后呢,之前听你一直说什么扩欧,究竟怎么用它算 x 和 y啊.
求解此类方程的方法有很多,其中我们常用扩展欧几里得算法解决此类问题.啊又是大白废话

扩展欧几里得算法

我们想一下我们在 gcd 算法进行中都干了些什么.

最终,我们算出了 gcd(a,b) . gcd(a,b)的最后一层,为 gcd(r,0)=r=gcd(a,b).此刻,有rx + 0y = r这样一个方程.显然,可以让x=1 ,而 y任意.然后我们再想一下,一般情况下.这时方程就是ax + by = m.我们在gcd中是这样递归的:

int gcd(int a,int b){
	if(!b)return a;
	return gcd(b,a%b);//重点
}

由此,扩欧的理论框架便定下来了.接下来是实现.
扩展欧几里得算法一般采用递归实现.当然也可以循环.这里给两种实现方法.

第一种.x,y放在全局变量中,或者类成员里.
按照结论递归即可.

ll exgcd(ll a,ll b){
    if(b==0){
        x=1;y=11451419;//我对自己的这个数字也很有想法啊(恼
        return a;
    }
    ll xx=exgcd(b,a%b);
    ll c=(x-(a/b)*y);
    x=y;y=c;
    return xx;
}

第二种,x,y放在参数里,就是我们最常见的交换参数的exgcd.
至于这样为啥是对的.很显然,x在下一层递归返回时是y’,y在下一层递归返回时是x’,由此可知正确.

ll exgcd(ll a,ll b,ll&x,ll&y){
    if(b==0){
        x=1;y=0;
        return a;
    }
    ll xx=exgcd(b,a%b,y,x);
    y-=(a/b)*x;
    return xx;
}

还有啥位运算gcd什么的奇技淫巧我就不发出来误导大家了,毕竟本蒟蒻自己都没学会.

由此,这道题成功被我们解决了.

代码

/*
Code by Azrl.
Date:2022-12-09 17:56:55
Address: LTYZ(E)
*/
#include<iostream>
#include<algorithm>
#include<cassert>
using namespace std;
typedef long long ll;
const ll mod = 998244353;
ll x,y;
ll a,b;
ll exgcd(ll a,ll b){
    if(b==0){
        x=1;y=11451419;
        return a;
    }
    ll xx=exgcd(b,a%b);
    ll c=(x-(a/b)*y);
    x=y;y=c;
    return xx;
}
inline void read(ll&x){
    x=0;char at=getchar();
    while(!isdigit(at))at=getchar();
    while(isdigit(at))(x=((x<<3)+(x<<1)+at-'0')/*%mod*/),at=getchar();

}
int main(){
    read(a);read(b);
    //P1082
    ll as = exgcd(a,b);
    x=(x%b+b)%b;
    cout<<x<<endl;

    return 0;
}

好让我们来另外一道题目开开胃.

【模板】有理数取余

Solution

我对这个数字是很有想法的(不是.

代码

/*
Code by Azrl.
Date:2022-12-09 17:55:31
*/

#include<iostream>
#include<algorithm>
#include<cassert>
using namespace std;
typedef long long ll;
const ll mod = 19260817;//对于这个数字,很有些想法
ll x,y;
ll a,b;
ll exgcd(ll a,ll b,ll&x,ll&y){
    if(b==0){
        x=1;y=0;
        return a;
    }
    ll xx=exgcd(b,a%b,y,x);
    y-=(a/b)*x;
    return xx;
}
inline void read(ll&x){
    x=0;char at=getchar();
    while(!isdigit(at))at=getchar();
    while(isdigit(at))(x=((x<<3)+(x<<1)+at-'0')/**/%mod/**/),at=getchar();

}
int main(){
    read(a);read(b);
    //P2613
    ll as = exgcd(b,mod,x,y);
    x=(x%mod+mod)%mod;
    cout<<((a*x)%mod)<<endl;

    return 0;
}

后记

话说我本来说星期四写完的,鸽了三天哎.
本文是2020年12月08日完成,但今天才成功录入至电脑,并载入博客.我太懒了 老实说数论是曾经我最不愿意面对的东西.因为数论,数学,都给我留下过很多悲伤的记忆wtcl.但经过高中生活到现在,我渐渐明白了,向着自己害怕的地方冲击,才会找到自身困惑的突破口,变得更勇敢更强.
同时,数论真的是个很美的东西.多花点时间感受一下,受益匪浅啊.
同时,照例欢迎您们来吊打蒟蒻,本文肯定有很多不足的地方罢.
还有@heiyedao,您站点的latex装好了吗,催更
这个星期刚经过了那个众所周知的风暴,都有点疲倦了,我就研究一下OI以外的东西.下周看看我更什么吧.
话说我还鸽着好几篇题解没搬运上来,啊
大家都加油.